Cálculo do elemento de aquecimento

Para determinar um dos principais parâmetros do fio do elemento de aquecimento - diâmetro d, m (mm), são utilizados dois métodos de cálculo: de acordo com a potência de superfície específica permitida PF e usando a tabela de cargas atuais.

Potência de superfície específica permitida PF= P⁄F,

onde P é a potência do aquecedor de fio, W;

F = π ∙ d ∙ l — área do aquecedor, m2; l — comprimento do fio, m.

De acordo com o primeiro método

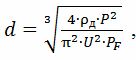
onde ρd — resistência elétrica do material do fio na temperatura real, Ohm • m; U é a tensão do fio aquecedor, V; PF - valores permitidos de potência de superfície específica para diferentes aquecedores:

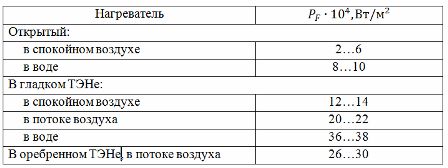
O segundo método usa uma tabela de cargas atuais (ver Tabela 1) compilada a partir de dados experimentais. Para usar a tabela indicada, é necessário determinar a temperatura de aquecimento calculada Tp em relação à temperatura real (ou admissível) do condutor Td pela relação:

Tr = Km ∙ Ks ∙ Td,

onde Km é o fator de instalação, levando em consideração a deterioração das condições de resfriamento do aquecedor devido à sua construção; Kc é o fator ambiente, considerando a melhoria das condições de resfriamento do aquecedor em comparação com um ambiente de ar estacionário.

Para um elemento de aquecimento feito de arame torcido em espiral, Km = 0,8 … 0,9; o mesmo, com base cerâmica Km = 0,6 ... 0,7; para um fio de placas de aquecimento e alguns elementos de aquecimento Km = 0,5 ... 0,6; para um condutor de piso elétrico, solo e elementos de aquecimento Km = 0,3 ... 0,4. Um valor menor de Km corresponde a um aquecedor de menor diâmetro, um valor maior a um diâmetro maior.

Ao operar em condições diferentes da convecção livre, Kc = 1,3 … 2,0 é considerado para elementos de aquecimento na corrente de ar; para elementos em água parada Kc = 2,5; no fluxo de água — Kc = 3,0 … 3,5.

Se a tensão Uph e a potência Pf do futuro aquecedor (projetado) forem definidas, então sua corrente (por fase)

Iph = Pph⁄Uph

De acordo com o valor calculado da corrente do aquecedor para a temperatura calculada necessária de seu aquecimento de acordo com a tabela 1, é encontrado o diâmetro necessário do fio de nicromo d e o comprimento necessário do fio, m, para a fabricação do aquecedor é calculado:

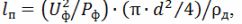
onde d é o diâmetro do fio selecionado, m; ρd é a resistência elétrica específica do condutor na temperatura real de aquecimento, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

onde αр— coeficiente de temperatura de resistência, 1/OS.

Para determinar os parâmetros da espiral de nicromo, pegue o diâmetro médio das voltas D = (6 … 10) ∙ d, o passo da espiral h = (2 … 4) ∙ d,

número de voltas

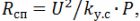
comprimento da hélice lsp = h ∙ n.

Ao calcular os elementos de aquecimento, deve-se lembrar que a resistência do fio espiral após pressionar o elemento de aquecimento

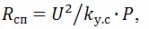
onde k (y.s) é um coeficiente que leva em conta a redução da resistência da espiral; de acordo com dados experimentais, k (s) = 1,25. Também deve ser levado em consideração que a potência de superfície específica do fio espiral é 3,5 ... 5 vezes maior que a potência de superfície específica do elemento de aquecimento tubular.

Em cálculos práticos do elemento de aquecimento, primeiro determine a temperatura de sua superfície Tp = To + P ∙ Rt1,

onde é a temperatura ambiente, °C; P é a potência do elemento de aquecimento, W; RT1 — resistência térmica no tubo — interface média, ОC / W.

Então a temperatura do enrolamento é determinada: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

onde Rt2 é a resistência térmica da parede do tubo, ОC / W; RT3 — resistência térmica da carga, ОC / W; Rp1 = 1⁄ (α ∙ F), onde α é o coeficiente de transferência de calor, W / (m ^ 2 • ОС); F — área do aquecedor, m2; Rt2 = δ⁄ (λ ∙ F), onde δ é a espessura da parede, m; λ — condutividade térmica da parede, W / (m • ОС).

Para mais informações sobre o dispositivo dos elementos de aquecimento, consulte aqui: Elementos de aquecimento. Dispositivo, seleção, operação, conexão de elementos de aquecimento

Tabela 1. Tabela de cargas atuais

Exemplo 1. Calcule o aquecedor elétrico na forma de uma espiral de fio de acordo com a potência de superfície específica permitida PF.

Doença.Potência do aquecedor P = 3,5 kW; tensão de alimentação U = 220 V; material do fio — nicromo Х20Н80 (uma liga de 20% de cromo e 80% de níquel), portanto a resistência elétrica específica do fio ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; coeficiente de temperatura de resistência αр = 16 ∙ 10 ^ (- 6) 1 /ОС; a espiral é aberta, na forma metálica, a temperatura de trabalho da espiral é Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Determine d, lp, D, h, n, lp.

Responder. Resistência da bobina: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohms.

Resistência elétrica específica em Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Encontre o diâmetro do fio:

Da expressão R = (ρ ∙ l) ⁄S obtemos l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), daí o comprimento do fio

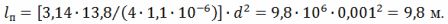
O diâmetro médio da volta em espiral é D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Passo da espiral h = 3 ∙ d = 3 ∙ 1 = 3 mm.

O número de voltas da espiral

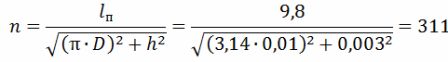
O comprimento da hélice é lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Exemplo 2. Calcular estruturalmente o aquecedor de resistência do fio ao determinar o diâmetro do fio d usando a tabela de cargas de corrente (consulte a tabela 1).

Doença. Potência do aquecedor de fio P = 3146 W; tensão de alimentação U = 220 V; material do fio — nicromo Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; hélice aberta localizada na corrente de ar (Km = 0,85, Kc = 2,0); temperatura operacional admissível do condutor Td = 470 ОС.

Determine o diâmetro d e o comprimento do fio lp.

Responder.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

A corrente do aquecedor projetada I = P⁄U = 3146⁄220 = 14,3 A.

De acordo com a tabela de cargas atuais (consulte a tabela 1) em Tр = 800 ОС e I = 14,3 A, encontramos o diâmetro e a seção transversal do fio d = 1,0 mm e S = 0,785 mm2.

Comprimento do fio lp = (R ∙ S) ⁄ρ800,

onde R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = 1,11 ∙ 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Além disso, se necessário, semelhante ao primeiro exemplo, D, h, n, lsp podem ser definidos.

Exemplo 3. Determine a tensão permitida do aquecedor elétrico tubular (TEN).

Condição... A bobina do elemento de aquecimento é feita de fio de nicromo com diâmetro d = 0,28 mm e comprimento l = 4,7 M. O elemento de aquecimento está no ar parado com uma temperatura de 20 °C. Características do nicromo: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. O comprimento da parte ativa do invólucro do elemento de aquecimento é La = 40 cm.

O elemento de aquecimento é liso, diâmetro externo dob = 16 mm. Coeficiente de transferência de calor α = 40 W / (m ^ 2 ∙ ° C). Resistências térmicas: enchimento RT3 = 0,3 ОС / W, paredes da caixa Rт2 = 0,002 ОС / W.

Determine qual tensão máxima pode ser aplicada ao elemento de aquecimento para que a temperatura da bobina Tsp não exceda 1000 ℃.

Responder. Temperatura do elemento de aquecimento do elemento de aquecimento

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

onde é a temperatura do ar ambiente; P é a potência do elemento de aquecimento, W; RT1 — resistência térmica de contato da interface tubo-meio.

Potência do elemento de aquecimento P = U ^ 2⁄R,

onde R é a resistência da bobina de aquecimento.Portanto, podemos escrever Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), onde a tensão no elemento de aquecimento

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Encontre R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

onde ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ∙ 10 ^ ( — 6) Ohm • m.

Então R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Resistência térmica de contato RT1 = 1⁄ (α ∙ F),

onde F é a área da parte ativa da casca do elemento de aquecimento; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Encontre Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Determine a tensão do elemento de aquecimento U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Se a tensão nominal indicada no elemento de aquecimento for 220 V, então a sobretensão em Tsp = 1000 OS será de 5,6% ∙ Un.