Força de tração de eletroímãs

A força com a qual um eletroímã atrai materiais ferromagnéticos depende do fluxo magnético F ou, de forma equivalente, da indução B e da área da seção transversal do eletroímã S.

A força de pressão do eletroímã é determinada pela fórmula

F = 40550 ∙ B ^ 2 ∙ S,

onde F é a força de pressão do eletroímã, kg (a força também é medida em newtons, 1 kg = 9,81 N ou 1 N = 0,102 kg); B — indução, T; S é a área da seção transversal do eletroímã, m2.

Exemplos de

1. O eletroímã da torneira é um circuito magnético (Fig. 1). Qual é a força de elevação de um eletroímã de guindaste em ferradura, se a indução magnética é B = 1 T e a área da seção transversal de cada pólo do eletroímã é S = 0,02 m2 (Fig. 1, b)? Despreze o efeito do espaço entre o eletroímã e a armadura.

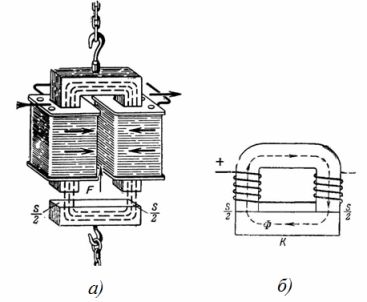
Arroz. 1. Eletroímã de elevação

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

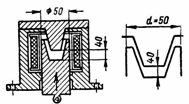
2. Um eletroímã circular de aço tem as dimensões mostradas na fig. 2, a e b. A força de elevação do eletroímã é 3 T. Determine a área da seção transversal do núcleo do eletroímã, n. p. e o número de voltas da bobina em uma corrente de magnetização I = 0,5 A.

Arroz. 2. Eletroímã redondo

O fluxo magnético passa pelo núcleo interno circular e retorna pelo corpo cilíndrico. As áreas das seções transversais do núcleo Sc e do revestimento Sk são aproximadamente as mesmas, portanto os valores de indução no núcleo e no revestimento são praticamente os mesmos:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

A indução necessária no eletroímã é determinada pela fórmula F = 40550 ∙ B ^ 2 ∙ S,

onde B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

A tensão nesta indução é encontrada na curva de magnetização do aço fundido:

H = 180 A/m.

O comprimento médio da linha de campo (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Força de magnetização I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

Na verdade n. s, ou seja, a corrente e o número de voltas, deve ser muitas vezes maior, pois existe um inevitável entreferro entre o eletroímã e a armadura, o que aumenta significativamente a resistência magnética do circuito magnético. Portanto, o entreferro deve ser levado em consideração ao calcular os eletroímãs.

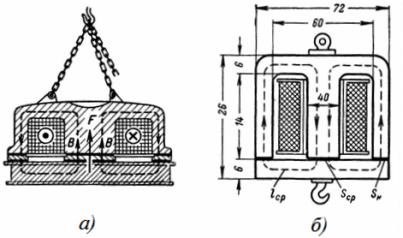
3. A bobina do eletroímã da torneira tem 1350 voltas, passando por ela uma corrente I = 12 A. As dimensões do eletroímã são mostradas na fig. 3. Que peso o eletroímã levanta a uma distância de 1 cm da armadura e que peso ele pode suportar após a gravidade?

Arroz. 3. Bobina eletromagnética

A maior parte de N. com I ∙ ω é gasta na condução de fluxo magnético através do entreferro: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Força de magnetização I ∙ ω = 12 ∙ 1350 = 16200 A.

Como H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, então Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Portanto, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, ou seja, B = 1,012T.

Assumimos que a indução é B = 1 T, pois parte de n. c. I ∙ ω é gasto na condução de fluxo magnético em aço.

Vamos verificar este cálculo pela fórmula I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

O comprimento médio da linha magnética é: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

A intensidade Hc em B = 1 T (10000 Gs) é determinada a partir da curva de magnetização:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

A força de magnetização I ∙ ω = 16114 Av criando uma indução B = 1 T é praticamente igual ao n dado. v. I ∙ ω = 16200 Av.

A área total da seção transversal do núcleo e do cone é: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

O eletroímã atrairá uma carga de peso F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg de uma distância de 1 cm.

Como o entreferro praticamente desaparece após a atração da armadura, o eletroímã pode suportar uma carga muito maior. Neste caso, todo o n. c. I ∙ ω é gasto na condução de fluxo magnético apenas no aço, portanto I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Com essa tensão, o aço está praticamente saturado e a indução nele é de aproximadamente 2 T. O eletroímã atrai a armadura com uma força F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. O relé de sinal (pisca) consiste em um eletroímã blindado 1 com núcleo redondo e uma armadura tipo válvula 2, que, após fornecer corrente ao eletroímã, atrai e libera o pisca-pisca 3, que abre o dígito do sinal (Fig. 4).

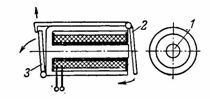
Arroz. 4. Eletroímã de blindagem

A força de magnetização é I ∙ ω = 120 Av, o entreferro é δ = 0,1 cm e a área total da seção transversal do eletroímã é S = 2 cm2. Estime a força de tração do relé.

A indutância B é determinada por aproximações sucessivas usando a equação I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Deixe n. c. Hc ∙ lc é 15% I ∙ ω, ou seja, 18 Av.

Então I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Portanto, encontramos a indução B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Depois de substituir o valor B na fórmula F = 40550 ∙ B ^ 2 ∙ S, obtemos:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

5. O solenóide do freio CC (Fig. 5) tem uma armadura de pistão com um batente cônico. A distância entre a armadura e o núcleo é de 4 cm, o diâmetro de trabalho (núcleos com área de contato circular) d = 50 mm. A armadura é puxada para dentro da bobina com uma força de 50 kg. O comprimento da linha média de força lav = 40 cm Determine n. pp. e a corrente da bobina se houver 3000 voltas.

Arroz. 5. Solenóide do freio CC

A área da seção de trabalho do eletroímã é igual à área de um círculo com diâmetro d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

A indução B necessária para criar uma força F = 50 kg é encontrada na equação F = 40550 ∙ B ^ 2 ∙ S,

onde B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Força de magnetização I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Determinamos a força de magnetização para o aço Hc ∙ lc de forma simplificada, com base no fato de ser 15% I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Av.

Corrente de magnetização I = (I ∙ ω) / ω = 30000/3000 = 10 A.