Cálculo de potenciômetro e shunt composto

Conceitos e fórmulas

Um potenciômetro é uma resistência variável com um controle deslizante incluído conforme mostrado na fig.

Para mais detalhes, consulte - Potenciômetros e suas aplicações

Uma tensão U é aplicada aos pontos 1 e 2. Uma tensão ajustável é removida dos pontos 2 e 3, cujo valor é menor que U e depende da posição do controle deslizante. Os divisores de tensão têm um esquema semelhante, mas não são ajustáveis ​​e não possuem um controle deslizante móvel.

Potenciômetros, divisores de tensão e shunts complexos são calculados usando leis de Kirchhoff, como o cálculo de circuitos convencionais com resistências.

Exemplos de

1. A tensão da fonte é U = 24 V, a resistência total do potenciômetro é r = 300 Ohm. O motor é montado separadamente de modo que r1 = 50 ohms. Que tensão U1 pode ser removida dos pontos 3 e 2 (Fig. 1)?

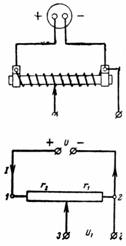
Arroz. 1.

A corrente I e a tensão U através da resistência r estão relacionadas pela fórmula I ∙ r = U.

O controle deslizante do potenciômetro separa parte da resistência, ou seja. a resistência r1. A queda de tensão entre os pontos 3 e 2 é igual a I ∙ r1 = U1.

Da relação da queda de tensão, obtemos a igualdade (I ∙ r1) / (I ∙ r) = U1 / U. Quanto maior a resistência r1, maior o valor da tensão U1 entre os pontos 3 e 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. O potenciômetro (Fig. 2) é carregado em uma lâmpada com resistência r = 100 Ohm. O potenciômetro é dividido por um controle deslizante em duas partes com r1 = 600 Ohm e r2 = 200 Ohm. Determine a tensão Ul e a corrente da lâmpada Il.

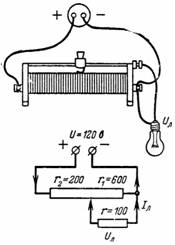
Arroz. 2.

A corrente I flui através da resistência r2 e a corrente Il flui através da lâmpada. Uma corrente I-Il flui através da resistência r1, o que cria uma tensão através da resistência r1 igual à tensão da lâmpada: (I-Il) ∙ r1 = Ul.

Por outro lado, a tensão da lâmpada é igual à tensão da fonte menos queda de voltagem na resistência r2: U-I ∙ r2 = Ul.

A corrente I é igual à tensão da fonte dividida pela resistência resultante da conexão série-paralelo das resistências:

I = U / (r2 + (r ∙ r1) / (r + r1)).

Substituímos a expressão para a corrente total da fonte na segunda equação:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Após a transformação, obtemos uma expressão para a tensão da lâmpada:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Se transformarmos esta expressão, partindo do fato de que Ul = Il ∙ r, obtemos uma expressão para a corrente da lâmpada:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Substitua os valores numéricos nas equações resultantes:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0,36 A.

3. Calcule a tensão Up e a corrente Ip do dispositivo de medição que está conectado a uma parte do potenciômetro. O dispositivo tem uma resistência de r = 1000 Ohm. O ponto de ramificação divide a resistência do divisor em r2 = 500 ohms e r1 = 7000 ohms (Fig. 3).Tensão nos terminais do potenciômetro U = 220 V.

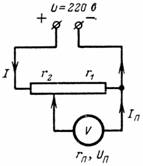
Arroz. 3.

Usando as fórmulas obtidas anteriormente, podemos escrever que a corrente que flui pelo dispositivo é:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14 A.

Up = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Calcule a tensão do dispositivo Up, se ele consome uma corrente Ip = 20 mA e está conectado a um potenciômetro dividido em resistências r2 = 10 ^ 4 Ohm e r1 = 2 ∙ 10 ^ 4 Ohm (Fig. 3).

A tensão total no divisor de tensão é igual à soma das quedas de tensão em suas partes (através das resistências r1 e r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Acima

A corrente da fonte é ramificada no ponto de contato do motor: I = I1 + Ip; I = Upn / r1 + In.

Substituímos o valor da corrente I na equação da tensão:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Portanto, a tensão do dispositivo Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Substitua os valores numéricos: Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Uma fonte de corrente contínua com tensão U = 120 V alimenta os circuitos anódicos do receptor de rádio através de um potenciômetro (divisor de tensão), que junto com o filtro possui uma resistência de r = 10000 Ohm. A tensão U1 é removida pela resistência r2 = 8000 Ohm. Calcule a tensão anódica sem carga e com corrente de carga I = 0,02 A (Fig. 4).

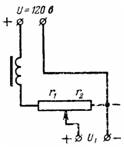
Arroz. 4.

O primeiro caso é semelhante ao exemplo 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

O segundo caso é semelhante ao exemplo 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Ao carregar, a tensão cairá de 96 para 64 V.Se for necessária mais tensão, o controle deslizante deve ser movido para a esquerda, ou seja, a resistência r2 deve ser aumentada.

6. As tensões Ua e Ub são removidas pelo divisor de tensão. A resistência total do divisor de tensão conectado à tensão U1 = 220 V é r = 20.000 Ohm. Qual é a tensão Ua na resistência r3 = 12000 Ohm com consumo de corrente Ia = 0,01 A e a tensão Ub na resistência r2 + r3 = 18000 Ohm com consumo de corrente Ib = 0,02 A (Fig. 5).

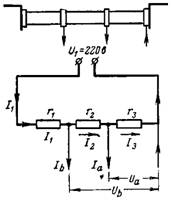
Arroz. 5.

Resistência de tensão r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

A tensão Ub é igual à soma da queda de tensão Ua na resistência r3 e a queda de tensão na resistência r2. A queda de tensão na resistência r2 é igual a I2 ∙ r2. Corrente I2 = Ia + I3. A corrente I3 pode ser calculada como no exemplo 1:

I3 = (220-80-40) / 20.000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Tensão Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

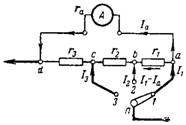
7. Calcule o shunt combinado para o miliamperímetro de forma que em diferentes posições da chave tenha as seguintes faixas de medição: I1 = 10 mA; I2 = 30mA; I3 = 100mA. O diagrama de conexão do shunt é mostrado na fig. 6. Resistência interna do dispositivo ra = 40 Ohm. Faixa de medição intrínseca de miliamperímetro 2 mA.

Arroz. 6.

Ao medir a corrente I≤2mA, o shunt é desligado.

a) Ao medir a corrente I = 10 mA, a chave está na posição 1 e uma corrente de 10-2 = 8 mA flui por todas as resistências shunt. A queda de tensão através da resistência shunt Ush e o dispositivo Ua entre os pontos d e a deve ser o mesmo

Ush = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Ao medir a corrente I2 = 30 mA, a chave está na posição 2. A corrente medida será dividida no ponto b. Na deflexão total do ponteiro do dispositivo, a corrente Ia = 2 mA passará pela resistência r1 e pelo dispositivo ra.

O restante da corrente I2-Ia passará pelas resistências r2 e r3. As correntes criarão a mesma queda de tensão nos dois ramos entre os pontos d e b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) De forma semelhante, faremos o cálculo ao aumentar a faixa de medição para I3 = 100 mA. A corrente I3-Ia fluirá através da resistência r3 e a corrente Ia através das resistências r1, r2, ra. A tensão em ambos os ramos é a mesma: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Obtivemos três equações com três valores desconhecidos das resistências r1, r2 e r3.

Multiplicamos todas as equações por 1000 e as convertemos:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Vamos somar a primeira e a terceira equações: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohm.

Vamos somar a primeira e a segunda equações: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohms.

Vamos substituir os resultados obtidos na primeira equação: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohms.

A exatidão do cálculo pode ser verificada substituindo os valores de resistência obtidos nas equações.