Processo oscilatório em engenharia elétrica e eletrônica, tipos de oscilações
Processo oscilatório — um processo com vários graus de repetibilidade. Todos os processos oscilatórios são divididos em 2 classes: periódicos e não periódicos. Em teoria, eles também usam uma classe intermediária - oscilações quase periódicas.
Um processo oscilatório é denominado periódico, no qual o valor que caracteriza esse processo, tomado a qualquer momento, após um certo período de tempo T tem o mesmo valor.
A função f(t), que é uma expressão matemática do processo oscilatório, é denominada periódica de período T se satisfaz a condição f(t + T) = f(t).
Entre a classe de processos oscilatórios periódicos, o papel principal é desempenhado por oscilações harmônicas ou senoidais, nas quais ocorre uma mudança em uma quantidade física com o tempo de acordo com a lei do seno ou cosseno. Seu registro geral é:
y = f (t) = aCos ((2π / T) t — φ),
onde a — amplitude das oscilações, φ é a fase da oscilação, 1 /T = f — frequência e 2πf = ω — frequência das vibrações cíclicas ou circulares.
Aplicação de oscilações senoidais e suas características:
Maneiras gráficas de exibir a corrente alternada
Uma função quase periódica correspondente a uma leitura de oscilações periódicas é definida pela condição:
| f · (t + τ) — f (t) | <= ε onde ε — atribui um valor a cada valor T.
A quantidade τ neste caso é chamada quase período. Se o valor ε for muito pequeno comparado ao valor médio de f(t) no tempo T, então a função quase periódica estará próxima da periódica.
As oscilações não periódicas são muito mais variadas do que as periódicas. Mas, na maioria das vezes, na automação, é necessário encontrar amortecimento ou aumento de oscilações senoidais.
As oscilações de acordo com a lei da senóide amortecida ou, como às vezes são chamadas, oscilações harmônicas amortecidas, podem ser representadas de uma forma geral:
x = Ae-δTcos·(ω + φ),
onde t é o tempo, A e φ são constantes arbitrárias. A notação geral da lei das oscilações harmônicas crescentes difere apenas no sinal do fator de amortecimento δ[1 segundo].
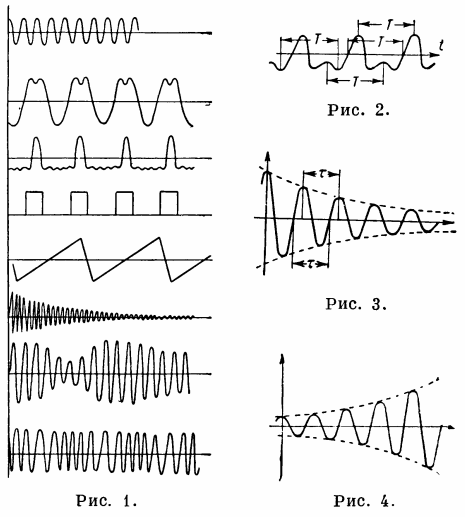
Figo. 1 — processo oscilante, Fig. 2. — processo periódico, figo. 3. — oscilações harmônicas decadentes, figo. 4. — aumento das oscilações harmônicas.
Um exemplo da aplicação do processo oscilatório é o circuito oscilatório mais simples.
Circuito oscilador (circuito elétrico) — um circuito elétrico passivo no qual podem ocorrer oscilações elétricas com uma frequência determinada pelos parâmetros do próprio circuito.
O circuito oscilante mais simples consiste na capacitância C e na indutância L. Na ausência de influência externa, amortece as oscilações com frequência εО = 1/2π√LC.
A amplitude das vibrações diminui com, por exemplo,-δT, onde δ é o coeficiente de amortecimento. Se δ> = eO, então as oscilações amortecidas no circuito tornam-se não periódicas.
Em eletrônica, a qualidade do circuito oscilante é determinada pelo fator de qualidade: Q = nf/δ... Quando uma força periódica externa atua no circuito oscilante, ocorrem oscilações forçadas nele. A amplitude das oscilações forçadas aumenta significativamente para circuitos de alto Q se a frequência da influência externa estiver próxima de eo (ressonância). Circuito oscilante é uma das partes principais em amplificadores ressonantes, geradores e outros dispositivos eletrônicos.
Veja também neste tópico: Aplicação de ressonância de tensão e ressonância de corrente
