Fontes de harmônicos em redes elétricas

Como os elementos não lineares estão invariavelmente presentes na elétrica moderna, especialmente nas redes industriais, como resultado, as curvas de corrente e as curvas de tensão são distorcidas, harmônicos mais altos aparecem nas redes.

Em primeiro lugar, a não sinusoidalidade se deve à presença de conversores estáticos, depois - geradores síncronos, máquinas de solda, lâmpadas fluorescentes, fornos a arco, transformadores, motores e outras cargas não lineares.

Matematicamente, a não senoidalidade das curvas de corrente e tensão pode ser representada como a soma do harmônico principal da frequência da rede e seus harmônicos superiores que são múltiplos dele. A análise harmônica resulta em uma série trigonométrica de Fourier, e os valores das frequências e fases dos harmônicos resultantes podem ser facilmente calculados usando a fórmula:

De fato, a combinação resultante de tensões e correntes não senoidais em uma rede trifásica pode ser assimétrica ou simétrica.Um sistema simétrico de tensões não senoidais para múltiplos de três harmônicos (k = 3n) leva à formação de um sistema de tensões de seqüência zero.

Além disso, em k = 3n + 1, o harmônico na rede trifásica gera um sistema simétrico de tensões de sequência negativa. Portanto, todo k-harmônico de um sistema simétrico de tensões não senoidais resulta em um sistema simétrico de tensões de fase de seqüência direta, reversa ou zero.

Na prática, no entanto, o sistema de tensões não senoidais de fase acaba sendo assimétrico. Então, núcleos magnéticos de transformadores trifásicos eles próprios, eles são não lineares e assimétricos, uma vez que os comprimentos dos caminhos magnéticos para as fases intermediária e final diferem por um fator de 1,9. Como resultado, os valores efetivos das correntes de magnetização da fase intermediária são 1,3 — 1,55 vezes menores que os valores das correntes de magnetização das fases finais.

Harmônicos assimétricos são decompostos em componentes simétricos quando cada k-harmônico forma um sistema assimétrico de tensões de fase e normalmente contém componentes de três sequências - zero, direto e reverso.

As redes trifásicas com neutro isolado são caracterizadas pela ausência de componentes de seqüência zero em cada uma das fases, desde que não haja faltas à terra. Como resultado, não há múltiplos de três harmônicos nas correntes de fase, mas há outros harmônicos que contêm componentes de sequência positiva e reversa.

Os retificadores de potência, via de regra, no lado CC possuem grandes indutâncias, que são enrolamentos de máquinas CC e reatores de suavização.Essas indutâncias são muitas vezes maiores que a indutância equivalente do lado da corrente alternada, portanto tais retificadores em relação à rede de corrente alternada se comportam como fontes de correntes harmônicas mais altas. A corrente direcionada para a rede com frequência harmônica tem um valor que independe dos parâmetros da rede de alimentação.

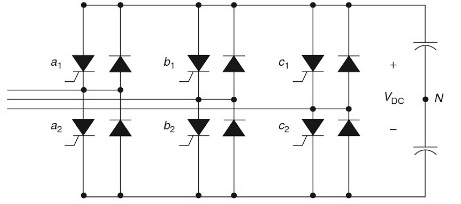
Para redes elétricas trifásicas, é característico o uso de retificadores trifásicos de onda completa para 6 válvulas como tais conversores, dos quais são chamados de seis pulsos ou seis fases. A curva de corrente para cada uma das fases neste caso pode ser descrita pela equação (para a corrente de uma fase A):

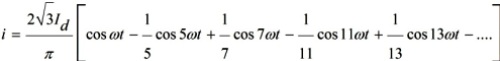
Pode-se ver que as correntes de fase contêm apenas harmônicos ímpares que não são múltiplos de três, e os sinais desses harmônicos se alternam: harmônicos positivos de 6k + 1ª ordem e harmônicos negativos de 6k-1ª ordem.

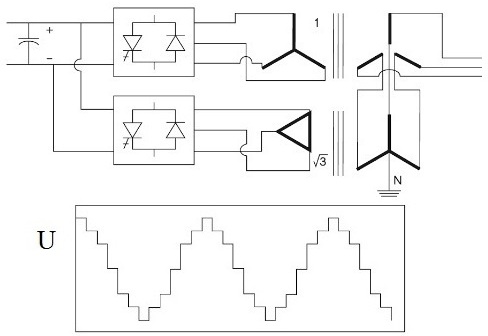
Se um retificador de doze fases for usado, quando um par de retificadores de seis fases for conectado a um par de transformadores trifásicos (as tensões secundárias são defasadas em pi / 6), então harmônicos de 12k + 1 e 12k- 1-ordens aparecerão, respectivamente.

Antes dos retificadores serem usados, apenas os transformadores e várias máquinas elétricas eram a principal fonte de harmônicos mais altos nas redes elétricas. Mas ainda hoje os transformadores são os elementos mais comuns das redes elétricas.

A razão pela qual os transformadores geram harmônicos mais altos é a curva de magnetização não linear dos circuitos magnéticos e a presença constante de loops de histerese… Uma curva de magnetização não linear e um loop de histerese geram distorções da corrente de magnetização sem carga senoidal original e o resultado são harmônicos mais altos na corrente que o transformador extrai da rede.

Os transformadores da classe 110 kV não têm mais do que 1% de corrente sem carga e os transformadores da classe 6-10 kV - não mais do que 2-3%. Estas são pequenas correntes e suas perdas ativas no circuito magnético são desprezíveis. É a curva de magnetização que importa, não o loop de histerese.

A curva de magnetização é simétrica e não há sequer harmônicos na expansão em série de Fourier. A distorção da corrente de magnetização é causada por harmônicos ímpares, entre os quais múltiplos de três. O terceiro harmônico é particularmente pronunciado, mas o quinto e o sétimo harmônicos também são os mais significativos.

Harmônicos EMF e harmônicos de corrente também são característicos de motores, tanto síncrono quanto assíncrono… Esses harmônicos são causados ​​pelos mesmos fenômenos que os harmônicos de corrente gerados por transformadores – a não linearidade da curva de magnetização dos materiais dos quais o estator e o rotor são feitos.

O espectro de frequência dos harmônicos de corrente de motores elétricos, como o de transformadores, inclui harmônicos ímpares, entre os quais estão obviamente múltiplos de três. Os mais significativos aqui são o 3º, 5º e 7º harmônicos.

Como no caso dos transformadores, cálculos aproximados permitem tomar a porcentagem de correntes do 3º, 5º e 7º harmônicos em 40% para o terceiro harmônico, 30% para o quinto harmônico e 20% para o sétimo harmônico (porcentagem de a corrente ociosa).