O princípio e os métodos de determinação indireta do fator de potência no circuito de corrente alternada

Fator de potência ou cosseno phi, em relação ao usuário de corrente alternada senoidal, é a relação entre o consumo de energia ativa P e a potência total S que é fornecida a esse usuário pela rede.

Potência total S, no caso geral, pode ser definido como o produto dos valores efetivos (raiz quadrada média) da corrente I e da tensão U no circuito considerado, e a potência ativa P - como irreversivelmente consumida pelo usuário para o operação de trabalho.

Potência reativa Q, embora faça parte da potência total, no entanto, não é consumida para realizar o trabalho, mas apenas participa da criação de campos elétricos e magnéticos alternados em alguns elementos do circuito do usuário.

exceto medição direta do fator de potência uso de dispositivos eletrodinâmicos - medidores de fase, existem métodos indiretos bastante lógicos que permitem entender matematicamente com precisão o valor dessa quantidade elétrica muito importante que caracteriza o usuário em um circuito de corrente alternada senoidal.

Vejamos os dados métodos indiretos em detalhes, Vamos entender o princípio da medição indireta do fator de potência.

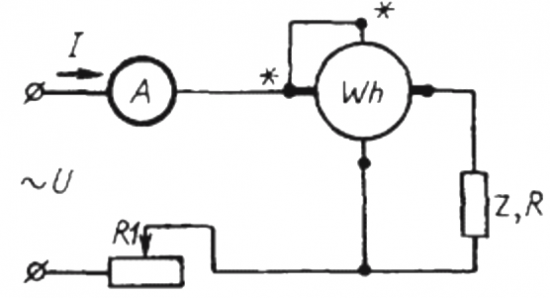
Método do voltímetro, amperímetro e wattímetro

Wattímetro eletrodinâmico com resistência ativa adicional no circuito de sua bobina móvel indica o valor da potência extremamente ativa consumida no circuito CA P.

Se agora, usando um voltímetro e um amperímetro, medirmos os valores médios da corrente I e da tensão U atuando no circuito da carga em estudo, multiplicando esses dois parâmetros, obteremos apenas a potência total S .

Então, o fator de potência (cosseno phi) de uma determinada carga pode ser facilmente encontrado usando a fórmula:

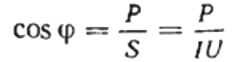
Aqui, se desejar, você também pode encontrar o valor da potência reativa Q, a resistência total do circuito z lei de ohm, bem como resistência ativa e reativa, simplesmente construindo ou representando um triângulo de resistência e, em seguida, usando o teorema de Pitágoras:

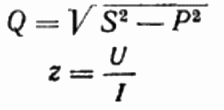
Método do contador e amperímetro

Para usar este método, é necessário montar um circuito no qual o mais simples seja conectado em série com a carga Z e o amperímetro medidor de eletricidade qu.

Para um determinado período de tempo t, da ordem de um minuto, será necessário calcular o número de rotações do disco N, que mostrará a quantidade de energia ativa gasta durante um determinado tempo (ou seja, levando em consideração o fator de potência).

Aqui: o número de rotações do disco N, o coeficiente k é a quantidade de energia por revolução, I e U são a corrente rms e a tensão respectivamente, t é o tempo para contar as rotações, cosseno phi é o fator de potência:

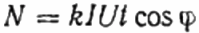
Então, em vez do usuário Z estudado, a carga ativa R é incluída no circuito através do mesmo contador, mas não diretamente, mas através do reostato R1 (obtendo a mesma corrente I do primeiro caso, com o usuário Z). O número de revoluções do disco N1 é mantido pelo mesmo tempo t. Mas aqui, como a carga está ativa, o cosseno phi (fator de potência) certamente é igual a 1. Portanto:

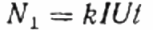
Em seguida, a relação de rotações do contador de disco é registrada para o mesmo período de tempo no primeiro e segundo casos. Isso será cosseno phi, ou seja, o fator de potência da primeira carga (relativo a uma carga puramente ativa com o mesmo atual):

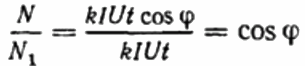
Método de três amperímetros

Para determinar o fator de potência em um circuito de corrente senoidal usando três amperímetros, você deve primeiro montar o seguinte circuito:

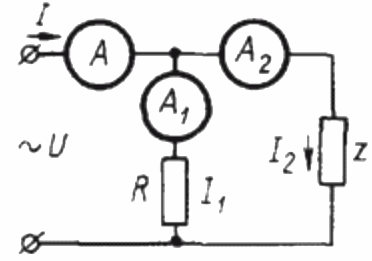
Aqui Z é uma carga cujo fator de potência deve ser determinado e R é uma carga puramente ativa.

Como a carga R é puramente ativa, a corrente I1 em qualquer instante de tempo está em fase com a tensão alternada aplicada a esta carga U. Neste caso, a corrente I é igual à soma geométrica das correntes I1 e I2. Agora vamos construir com base nesta posição um diagrama vetorial das correntes:

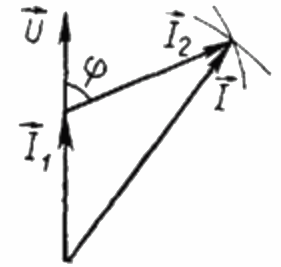
No diagrama vetorial das correntes, o ângulo agudo entre a corrente I1 e a corrente I2 é o ângulo phi, cujo cosseno (na verdade, o valor do fator de potência) pode ser encontrado em uma tabela especial de valores ​​de funções trigonométricas ou calculadas pela fórmula:

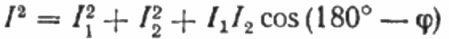
A partir daqui podemos expressar o cosseno phi, ou seja, o fator de potência desejado:

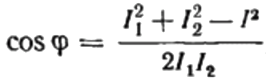
O sinal do fator de potência encontrado («+» ou «-«) indicará a natureza da carga. Se o fator de potência (cosseno phi) for negativo, a carga é de natureza capacitiva. Se o fator de potência for um valor positivo, a natureza da carga é indutiva.