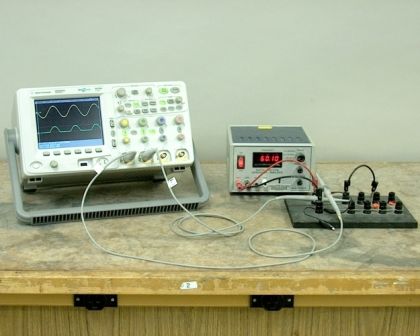
corrente de impulso

Em vários dispositivos eletrônicos, por exemplo, em equipamentos eletrônicos e semicondutores, ou seja, em amplificadores, retificadores, rádios, geradores, televisores, bem como em microfones de carbono, telégrafos e muitos outros dispositivos, são amplamente utilizadas correntes e tensões de ondulação ... para não repetir o raciocínio duas vezes, falaremos apenas de correntes, mas tudo que está relacionado a correntes vale também para tensões.

As correntes pulsantes que têm uma direção constante, mas mudam seu valor, podem ser diferentes. Às vezes, o valor atual muda do maior para o menor valor diferente de zero. Em outros casos, a corrente é reduzida a zero. Se circuito de corrente contínua é interrompido em uma certa frequência, então, por alguns intervalos de tempo, não há corrente no circuito.

Na fig. 1 mostra gráficos de várias correntes de onda. Na fig. 1, a, b, a mudança nas correntes ocorre de acordo com curva senoidal, mas essas correntes não devem ser consideradas correntes alternadas senoidais, pois a direção (sinal) da corrente não muda. Na fig.1, c mostra uma corrente que consiste em pulsos separados, ou seja, "choques" de corrente de curta duração, separados uns dos outros por pausas de maior ou menor duração, e é freqüentemente chamada de corrente pulsada. Diferentes correntes pulsadas diferem umas das outras na forma e duração dos pulsos, bem como na taxa de repetição.

É conveniente considerar uma corrente pulsante de qualquer tipo como a soma de duas correntes - direta e alternada, chamadas correntes de termo ou componentes. Qualquer corrente pulsante tem componentes DC e AC. Isso parece estranho para muitos. Afinal, uma corrente pulsante é uma corrente que flui o tempo todo em uma direção e muda de valor.

Como você pode dizer que contém corrente alternada que muda de direção? No entanto, se duas correntes - direta e alternada - passarem simultaneamente pelo mesmo fio, verifica-se que uma corrente pulsante fluirá nesse fio (Fig. 2). Neste caso, a amplitude da corrente alternada não deve exceder o valor da corrente contínua. Correntes contínuas e alternadas não podem fluir separadamente através do fio. Eles se somam a um fluxo geral de elétrons que tem todas as propriedades de uma corrente pulsante.

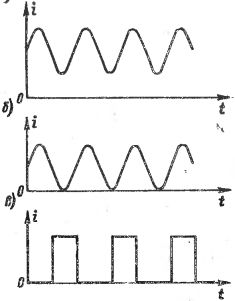
Arroz. 1. Gráficos de várias correntes de onda

A adição de correntes AC e DC pode ser mostrada graficamente. Na fig. 2 mostra os gráficos de uma corrente contínua igual a 15 mA e uma corrente alternada com amplitude de 10 mA. Se somarmos os valores dessas correntes para pontos individuais no tempo, levando em consideração as direções (sinais) das correntes, obtemos o gráfico de corrente de onda mostrado na fig. 2 com uma linha em negrito. Essa corrente varia de um mínimo de 5 mA a um máximo de 25 mA.

A adição de correntes considerada confirma a validade da representação da corrente pulsante como uma soma de correntes contínuas e alternadas. A exatidão dessa representação também é confirmada pelo fato de que, com a ajuda de alguns dispositivos, é possível separar os componentes dessa corrente uns dos outros.

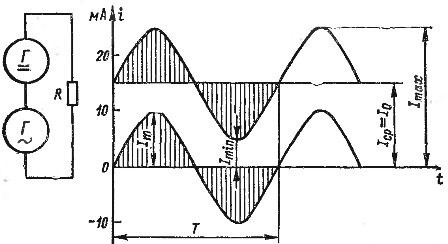
Arroz. 2. Obtenção de uma corrente pulsante somando corrente contínua e alternada.

Deve-se enfatizar que qualquer corrente sempre pode ser representada como uma soma de várias correntes. Por exemplo, uma corrente de 5 A pode ser considerada a soma das correntes 2 e 3 A fluindo em uma direção, ou a soma das correntes 8 e 3 A fluindo em direções diferentes, ou seja, em outras palavras, a diferença entre as correntes 8 e 3 A. Não é difícil encontrar outras combinações de duas ou mais correntes dando um total de 5 A.

Aqui há uma semelhança completa com o princípio de adição e decomposição de forças. Se duas forças igualmente direcionadas agem sobre qualquer objeto, elas podem ser substituídas por uma força comum. As forças que atuam em direções opostas podem ser substituídas por uma unidade de diferença. Por outro lado, uma determinada força sempre pode ser considerada a soma das forças correspondentes de mesma direção ou a diferença entre forças de direção oposta.

Não é necessário decompor correntes alternadas contínuas ou senoidais em correntes componentes. Se substituirmos a corrente pulsante pela soma das correntes contínua e alternada, aplicando as conhecidas leis das correntes contínua e alternada a essas correntes componentes, é possível resolver muitos problemas e fazer os cálculos necessários relacionados à corrente pulsante.

O conceito de corrente pulsante como uma soma de correntes contínuas e alternadas é convencional.Obviamente, não se pode presumir que, em determinados intervalos de tempo, as correntes contínua e alternada realmente fluam uma em direção à outra ao longo do fio. Na verdade, não há dois fluxos opostos de elétrons.

Na realidade, uma corrente pulsante é uma única corrente que muda de valor ao longo do tempo. É mais correto dizer que a tensão pulsante ou EMF pulsante pode ser representada como a soma dos componentes constantes e variáveis.

Por exemplo, na FIG. 2 mostra como algebricamente a fem constante de um gerador é adicionada à fem variável de outro gerador. Como resultado, temos um EMF pulsante que causa a corrente pulsante correspondente. Condicionalmente, porém, pode-se considerar que um EMF constante cria uma corrente contínua no circuito e um EMF alternado - uma corrente alternada que, quando somada, forma uma corrente pulsante.

Cada corrente pulsante pode ser caracterizada pelos valores máximos e mínimos de Itax e Itin, bem como suas componentes constantes e variáveis. A componente constante é denotada por I0. Se o componente alternado é uma corrente senoidal, então sua amplitude é denotada por It (todas essas quantidades são mostradas na Fig. 2).

Não deve ser confundido com It e Itax. Além disso, o valor máximo da onda de corrente Imax não deve ser chamado de amplitude. O termo amplitude geralmente se refere apenas a correntes alternadas. Em relação à corrente pulsante, podemos falar apenas sobre a amplitude de seu componente variável.

O componente constante da corrente pulsante pode ser chamado de valor médio Iav, ou seja, o valor médio aritmético. De fato, se considerarmos as mudanças em um período da corrente pulsante mostrada na Fig.2, vê-se claramente o seguinte: na primeira metade do ciclo, vários valores são adicionados à corrente de 15 mA variando o componente de corrente, variando de 0 a 10 mA e voltando a 0, e na segunda metade -ciclo, exatamente os mesmos valores de corrente são subtraídos dos 15 mA atuais.

Portanto, a corrente de 15 mA é realmente o valor médio. Como a corrente é a transferência de cargas elétricas através da seção transversal do fio, então Iav é o valor de uma corrente contínua que em um período (ou por um número inteiro de períodos) carrega a mesma quantidade de eletricidade que essa corrente pulsante .

Para corrente alternada senoidal, o valor de Iav por período é zero porque a quantidade de eletricidade que passa pela seção transversal do condutor em meio período é igual à quantidade de eletricidade que passa na direção oposta durante outro meio período. Nos gráficos de correntes que mostram a dependência da corrente i do tempo t, a quantidade de eletricidade transportada pela corrente é expressa pela área da figura delimitada pela curva de corrente, pois a quantidade de eletricidade é determinada pela produto que ele.

Para uma corrente senoidal, as áreas das meias ondas positivas e negativas são iguais.Na corrente pulsante mostrada na fig. 2, durante o primeiro semestre, a quantidade de eletricidade transportada pelo componente AC é adicionada à quantidade de eletricidade transportada pela corrente Iav (área sombreada na figura). E durante o segundo meio ciclo, exatamente a mesma quantidade de eletricidade é retirada. Como resultado, a mesma quantidade de eletricidade é transferida durante todo o período como com uma única corrente contínua Iav, ou seja, a área do retângulo Iav T é igual à área delimitada pela curva de corrente de onda.

Assim, a componente constante ou o valor médio da corrente é determinado pela transferência de cargas elétricas através da seção transversal do fio.

A equação atual mostrada na Fig. 2 deve obviamente ser escrito da seguinte forma:

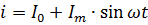
A potência da corrente pulsante deve ser calculada como a soma das potências de suas correntes componentes. Por exemplo, se a corrente mostrada na Fig. 2, passa por um resistor de resistência R, então sua potência é

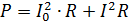
onde I = 0,7Im é o valor rms do componente variável.

Você pode introduzir o conceito do valor rms da corrente de onda Id. A potência é calculada da maneira usual:

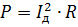
Igualando esta expressão à anterior e reduzindo-a a R, obtemos:

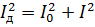
As mesmas relações podem ser obtidas para tensões.