Teoria dos autômatos, autômatos finitos
A estrutura, o design e o princípio de operação de várias máquinas são amplamente determinados por sua finalidade funcional. Distinguir entre máquinas tecnológicas, de transporte, computacionais, militares e outras. Complexos automáticos inteiros projetados para executar processos tecnológicos complexos são amplamente introduzidos em vários setores. Os autômatos são projetados e construídos para executar várias funções lógicas (máquinas lógicas).
teoria dos autômatos — seção de cibernética, que surgiu sob a influência dos requisitos da tecnologia de computadores digitais e máquinas de controle. Autômatos discretos estudados na teoria dos autômatos são modelos abstratos de sistemas reais (tanto técnicos quanto biológicos) que processam informações discretas (digitais) em intervalos de tempo discretos.
A teoria dos autômatos é baseada em conceitos matemáticos precisos que formalizam ideias intuitivas sobre o funcionamento (comportamento) do autômato e sobre sua estrutura (estrutura interna).
Neste caso, a transformação da informação é sempre entendida como uma operação que transforma sequências de entrada compostas por letras do alfabeto de entrada em sequências de saída compostas por letras do alfabeto de saída.
O aparato da lógica matemática, álgebra, teoria da probabilidade, combinatória e teoria dos grafos é amplamente utilizado.
O problema com a teoria dos autômatos em algumas de suas partes (teoria estrutural dos autômatos) cresceu da teoria dos circuitos de contato de relé, que começou a tomar forma no final da década de 1930. inclusive métodos de álgebra lógica.

Na teoria estrutural de autômatos são estudados diferentes tipos de esquemas, projetados para descrever como um autômato complexo é criado a partir de componentes (elementos) mais simples devidamente conectados em um sistema.
Outra direção, chamada de teoria abstrata dos autômatos, estuda o comportamento dos autômatos (ou seja, a natureza da transformação da informação realizada por eles), abstraindo das especificidades de sua estrutura interna, e surgiu na década de 1950.
No âmbito da teoria abstrata dos autômatos, o conteúdo dos conceitos "autômato" e "máquina" é essencialmente esgotado pela descrição padrão da transformação da informação que é realizada por um autômato. Tal transformação pode ser determinística, mas também pode ser de natureza probabilística.
As mais estudadas são as máquinas determinísticas (autômatos), que incluem os autômatos finitos — o principal objeto de estudo da teoria dos autômatos.
Uma máquina de estado finito é caracterizada por uma quantidade limitada de memória (o número de estados internos) e é definida usando uma função de transição.Com alguma idealização razoável, todas as máquinas matemáticas modernas e até mesmo o cérebro, do ponto de vista de seu funcionamento, podem ser considerados como autômatos finitos.
Os termos "máquina seqüencial", "Milly automaton", "Moore automaton" são usados na literatura (e não uniformemente por todos os autores) como sinônimos do termo "finite automaton" ou para enfatizar certas características nas funções de transição de um finito autômato.
Autômatos com memória ilimitada é uma máquina de Turing capaz de realizar (potencialmente) qualquer transformação de informação eficiente. O conceito de "máquina de Turing" surgiu antes do conceito de "máquina de estado finito" e é estudado principalmente na teoria dos algoritmos.
A teoria dos autômatos abstratos está intimamente relacionada com as teorias algébricas bem conhecidas, por exemplo, a teoria dos semigrupos. Do ponto de vista aplicado, são interessantes os resultados que caracterizam a transformação da informação em um autômato em termos de tamanho de memória.
É o caso, por exemplo, de problemas com experimentos sobre autômatos (trabalhos de E.F. Moore, etc.), onde uma ou outra informação sobre as funções de transição do autômato ou sobre a capacidade de sua memória é obtida a partir dos resultados do experimentos.
Outra tarefa é calcular os períodos das sequências de saída, com base nas informações disponíveis sobre o tamanho da memória do autômato e os períodos das sequências de entrada.
De grande importância é o desenvolvimento de métodos para minimizar a memória de máquinas de estados finitos e estudar seu comportamento em ambientes aleatórios.
Na teoria dos autômatos abstratos, o problema de síntese é o seguinte.Em termos de alguma linguagem claramente formalizada, as condições são escritas para o comportamento do autômato projetado (para o evento representado no autômato). Neste caso, é necessário desenvolver métodos que de acordo com cada condição escrita:
1) descobrir se existe tal máquina de estado que a informação por ela transformada atenda a essa condição;
2) se sim, então as funções de transição de tal máquina de estado finito são construídas ou seu tamanho de memória é estimado.
A solução da tarefa de síntese em tal formulação pressupõe a criação preliminar de uma linguagem conveniente para registrar as condições operacionais de um autômato com algoritmos convenientes para a transição de funções de registro para funções transitivas.
Na teoria estrutural de autômatos, o problema de síntese consiste em construir uma cadeia de elementos de um determinado tipo que realize um autômato finito dado por suas funções de transição. Nesse caso, eles geralmente estabelecem algum critério de otimalidade (por exemplo, o número mínimo de elementos) e buscam obter um esquema ótimo.
Como se viu mais tarde, isso significa que alguns dos métodos e conceitos desenvolvidos anteriormente em relação aos circuitos de contato de relé são aplicáveis a circuitos de outro tipo.
Em conexão com o desenvolvimento de tecnologias eletrônicas, os mais difundidos são os esquemas de elementos funcionais (redes lógicas). Um caso especial de redes lógicas são as redes neurais abstratas, cujos elementos são chamados de neurônios.
Muitos métodos de síntese foram desenvolvidos, dependendo do tipo de circuitos e da transformação da informação a que se destinam (Síntese de dispositivos de relé).
Olhar -Minimização de circuitos combinacionais, mapas de Carnot, síntese de circuitos
Máquina de estados finitos — um modelo matemático de um sistema de controle com um tamanho de memória fixo (incapaz de aumentar durante a operação).
O conceito de uma máquina de estado finito é uma abstração matemática que caracteriza as características gerais de um conjunto de sistemas de controle (por exemplo, um dispositivo de relé multiloop). Todos esses sistemas têm características comuns que são naturais para aceitar como a definição de um autômato finito.
Todo autômato completo tem uma entrada exposta a influências externas e elementos internos. Tanto para os elementos de entrada quanto para os internos, há um número fixo de estados discretos que eles podem assumir.
A mudança nos estados da entrada e dos elementos internos ocorre em momentos discretos no tempo, cujos intervalos são chamados de tiques. O estado interno (o estado dos internos) no final da fita é determinado inteiramente pelo estado interno e pelo estado da entrada no início da fita.
Todas as outras definições de autômato finito podem ser reduzidas a essa característica, em particular as definições que assumem que um autômato finito tem uma saída que depende do estado interno do autômato em um determinado momento.
Em termos de tal característica, a natureza de suas entradas e estados internos é irrelevante para a descrição de um autômato completo. Em vez de entradas e estados, você pode apenas olhar para seus números em uma numeração aleatória.
A máquina de estado será definida se a dependência de seu número de estado interno no número de estado interno anterior e no número de estado de entrada anterior for especificada. Tal tarefa pode ser na forma de uma mesa final.
Outra forma comum de definir um autômato completo é a construção do chamado diagramas de transição. Os estados de entrada geralmente são chamados simplesmente de entradas e os estados internos são simplesmente estados.
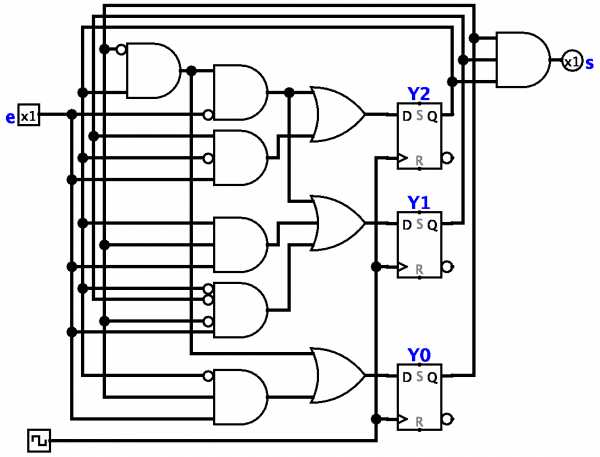
Uma máquina de estado finito pode ser um modelo tanto de dispositivos técnicos quanto de alguns sistemas biológicos. Os autômatos do primeiro tipo são, por exemplo, dispositivos de retransmissão e vários computadores eletrônicos, incl. controladores lógicos programáveis.
No caso de um dispositivo de relé, o papel dos estados de entrada é desempenhado por combinações de estados dos elementos sensíveis do dispositivo de relé (cada combinação desses estados é um «estado complexo», caracterizado por uma indicação de todos os elementos sensíveis de esses estados discretos que eles têm em um determinado momento). Da mesma forma, combinações de estados de elementos intermediários de um dispositivo de relé atuam como estados internos.
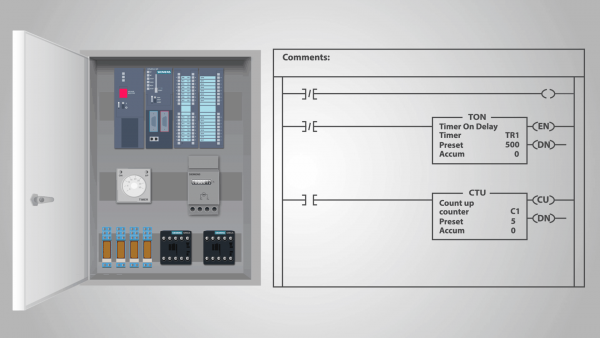
Um controlador lógico programável (PLC) é um exemplo de um dispositivo de ação de relé que pode ser chamado de máquina de estado autônoma.
De fato, uma vez que o programa foi inserido no PLC e o controlador começou a calcular, ele não é exposto a influências externas e cada estado subseqüente é completamente determinado por seu estado anterior. Podemos assumir que a entrada tem o mesmo estado em cada ciclo de clock.
Por outro lado, qualquer máquina de estado finito que tenha o único estado de entrada possível é naturalmente chamada de autônoma, pois nesse caso o ambiente externo não carrega nenhuma informação que controle seu comportamento.
Veja também:
O uso de sistemas microprocessados em engenharia elétrica a exemplo do uso de PLC