O que é força magnetomotriz, a lei de Hopkinson

Na segunda metade do século XIX, o físico inglês John Hopkinson e seu irmão Edward Hopkinson, desenvolvendo a teoria geral dos circuitos magnéticos, derivaram uma fórmula matemática chamada "fórmula de Hopkinson" ou lei de Hopkinson, que é um análogo da lei de Ohm (usada cálculo de circuitos elétricos).

Assim, se a lei clássica de Ohm descreve matematicamente a relação entre a corrente e a força eletromotriz (EMF), a lei de Hopkinson expressa de forma semelhante a relação entre o fluxo magnético e a chamada força magnetomotriz (MDF).

Como resultado, descobriu-se que força magnetomotriz é uma quantidade física que caracteriza a capacidade das correntes elétricas de criar fluxos magnéticos. E a lei de Hopkinson a esse respeito pode ser usada com sucesso nos cálculos de circuitos magnéticos, uma vez que o MDF em circuitos magnéticos é análogo ao EMF em circuitos elétricos. A data da descoberta da lei de Hopkinson é considerada 1886.

A magnitude da força magnetomotriz (MDF) é inicialmente medida em amperes ou, se estivermos falando de uma bobina com uma corrente ou um eletroímã, então, para conveniência dos cálculos, use sua expressão em voltas de amperes:

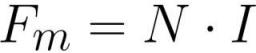
onde: Fm é a força magnetomotriz na bobina [ampere * volta], N é o número de voltas na bobina [volta], I é a quantidade de corrente em cada uma das voltas da bobina [ampere].

Se você inserir o valor do fluxo magnético aqui, a lei de Hopkinson para o circuito magnético assumirá a forma:

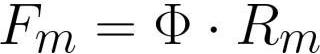
onde: Fm é a força magnetomotriz na bobina [ampere * volta], F é o fluxo magnético [weber] ou [henry * ampere], Rm é a resistência magnética do condutor de fluxo magnético [ampere * volta / weber] ou [ vira / henrique] .

A formulação textual da lei de Hopkinson era originalmente a seguinte: "em um circuito magnético não ramificado, o fluxo magnético é diretamente proporcional à força magnetomotriz e inversamente proporcional à resistência magnética total". Ou seja, esta lei determina a relação entre força magnetomotriz, relutância e fluxo magnético no circuito:

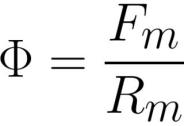
aqui: F é o fluxo magnético [weber] ou [henry * ampere], Fm é a força magnetomotriz na bobina [ampere * revolução], Rm é a resistência magnética do condutor de fluxo magnético [ampere * revolução / weber] ou [ vira / henrique] .

Aqui é importante notar que de fato a força magnetomotriz (MDF) tem uma diferença fundamental da força eletromotriz (EMF), que consiste no fato de que nenhuma partícula se move diretamente no fluxo magnético, enquanto a corrente que surge sob a ação de o EMF toma o movimento de partículas carregadas, por exemplo, elétrons em fios de metal. No entanto, a ideia do MDS ajuda a resolver os problemas de cálculo de circuitos magnéticos.

Considere, por exemplo, um circuito magnético não ramificado que inclua uma culatra de área transversal S, a mesma em todo o seu comprimento, e o material da culatra tenha uma permeabilidade magnética mu.

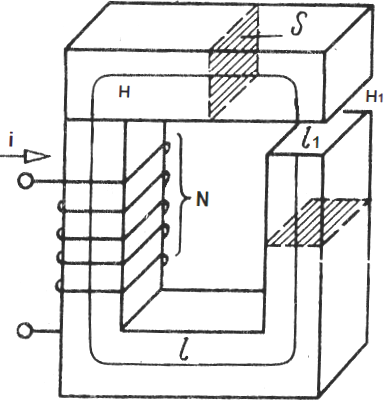
Folga na forquilha - material diferente, permeabilidade magnética qual mu1. A bobina colocada no jugo contém N voltas, uma corrente i flui através de cada uma das voltas da bobina. Aplicamos o teorema da circulação do campo magnético à linha central da culatra:

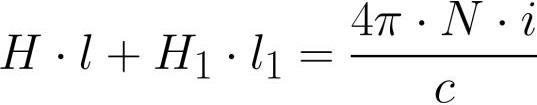
onde: H é a intensidade do campo magnético dentro da forquilha, H1 é a intensidade do campo magnético dentro da folga, l é o comprimento da linha central da indução da forquilha (sem a folga), l1 é o comprimento da folga.

Como o fluxo magnético dentro do jugo e dentro do gap tem o mesmo valor (devido à continuidade das linhas de indução magnética), depois de escrever Ф = BS e В = mu * H, anotaremos a intensidade do campo magnético com mais detalhes , e depois substitua isso na fórmula acima:

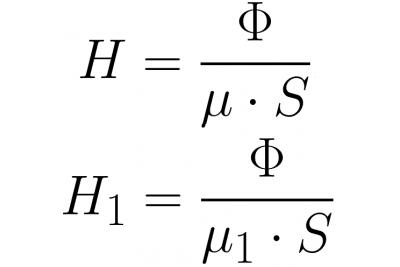
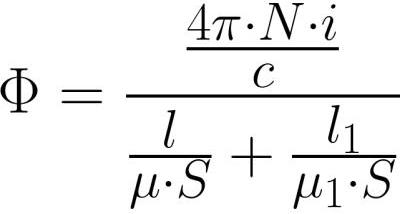
É fácil ver que, como o EMF na lei de Ohm para circuitos elétricos, o MDS

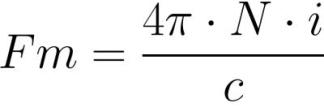
aqui desempenha o papel de força eletromotriz e resistência magnética

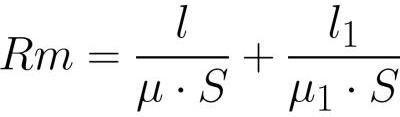
o papel da resistência (por analogia com a lei de Ohm clássica).