Oscilações contínuas e ressonância paramétrica

Vibrações contínuas — vibrações cuja energia não muda com o tempo. Em sistemas físicos reais, sempre existem causas que causam a transição da energia vibracional para a energia térmica (por exemplo, atrito em sistemas mecânicos, resistência ativa em sistemas elétricos).

Portanto, oscilações não amortecidas só podem ser obtidas desde que essas perdas de energia sejam repostas. Tal reabastecimento ocorre automaticamente em sistemas auto-oscilantes devido à energia de uma fonte externa. As oscilações eletromagnéticas contínuas são amplamente utilizadas. Diferentes geradores são usados ​​para obtê-los.

Para tornar as vibrações elétricas ou mecânicas (de um círculo oscilante ou pêndulo) não amortecidas, é necessário compensar as perdas de resistência ou fricção em todos os momentos.

Por exemplo, você pode atuar no circuito oscilante com um EMF alternado, que aumentará periodicamente a corrente na bobina e, consequentemente, manterá a amplitude da tensão no capacitor.Ou você pode empurrar o pêndulo de maneira semelhante, mantendo-o balançando harmoniosamente.

Como você sabe, a magnitude da energia do campo magnético da bobina do circuito oscilante está relacionada à sua indutância e corrente pela seguinte relação (a segunda fórmula éenergia do campo elétrico do capacitor mesmo contorno contorno)

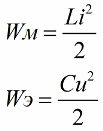
Fica claro pela primeira fórmula que se aumentarmos periodicamente a corrente na bobina, atuando no circuito EMF alternado, então (aumentando ou diminuindo o segundo fator na fórmula - corrente) iremos reabastecer periodicamente este circuito com energia.

Atuando no circuito estritamente no tempo com suas oscilações livres naturais, ou seja, na frequência de ressonância, obteremos o fenômeno da ressonância elétrica, pois está na frequência de ressonância sistema oscilante absorve mais intensamente a energia fornecida a ele.

Mas e se você alterar periodicamente não o segundo fator (não a corrente ou tensão), mas o primeiro fator - indutância ou capacitância? Nesse caso, o circuito também sofrerá uma variação em sua energia.

Por exemplo, empurrar periodicamente o núcleo para dentro e para fora da bobina ou empurrar para dentro e para fora do capacitordielétrico, - também obtemos uma mudança periódica muito definida na energia do circuito.

Escrevemos esta posição para uma mudança de unidade na indutância da bobina:

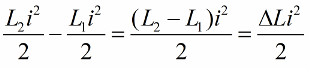
O efeito mais pronunciado da oscilação do circuito será se as mudanças de indutância forem feitas na hora certa. Por exemplo, se pegarmos o mesmo circuito a qualquer momento, quando alguma corrente i já estiver fluindo através dele, e introduzirmos um núcleo na bobina, a energia mudará na seguinte quantidade:

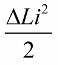
Agora deixe oscilações livres aparecerem no próprio circuito, mas no momento em que, após um quarto de período, a energia passar completamente para o capacitor e a corrente na bobina se tornar zero, removeremos abruptamente o núcleo da bobina A indutância retornará ao seu estado original, ao valor inicial L. Nenhum trabalho precisa ser gasto contra o campo magnético quando o núcleo é removido. Portanto, quando o núcleo foi empurrado para dentro da bobina, o circuito recebeu energia, pois trabalhamos, cujo valor:

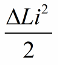
Após um quarto do período, o capacitor começa a descarregar, sua energia é novamente convertida em energia do campo magnético da bobina.Quando o campo magnético atingir a amplitude, pressionaremos novamente o núcleo com força. Novamente a indutância aumentou, aumentou na mesma quantidade.

E novamente, com corrente zero, retornamos a indutância ao seu valor original. Como resultado, se os ganhos de energia para cada meio ciclo excederem as perdas de resistência, a energia do loop aumentará o tempo todo e a amplitude de oscilação aumentará. Essa situação é expressa pela desigualdade:

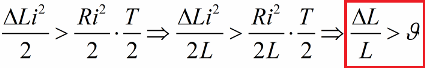
Aqui dividimos ambos os lados dessa desigualdade por L e anotamos a condição para a possibilidade de excitação paramétrica por saltos para um determinado valor do decremento logarítmico.

Recomenda-se alterar a indutância (ou capacitância) duas vezes por período, portanto a frequência da alteração do parâmetro (frequência de ressonância paramétrica) deve ser o dobro da frequência natural do sistema oscilante:

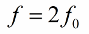
Assim, o caminho de excitação das oscilações no circuito apareceu sem a necessidade de alterar diretamente o EMF ou a corrente.A corrente flutuante inicial no circuito está sempre presente de uma forma ou de outra, e isso nem leva em consideração a interferência das oscilações de radiofrequência na atmosfera.

Se a indutância (ou capacitância) não mudar em saltos, mas harmonicamente, a condição para a ocorrência de oscilações será um pouco diferente:

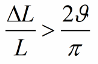
Como a capacitância e a indutância são parâmetros do circuito (como a massa de um pêndulo ou a elasticidade de uma mola), o método de excitar oscilações também é chamado de excitação paramétrica.

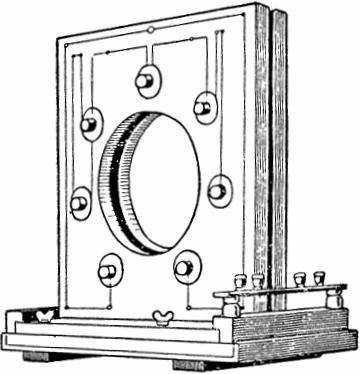
Este fenômeno foi descoberto e praticamente estudado no início do século XX pelos físicos soviéticos Mandelstam e Papalexi. Com base nesse fenômeno físico, eles construíram o primeiro gerador CA paramétrico com potência de 4 kW e indutância variável.

No projeto do gerador, sete pares de bobinas planas foram localizados em ambos os lados da estrutura, em cuja cavidade girava um disco ferromagnético com saliências. Quando o disco é levado a girar por um motor, suas saliências se movem periodicamente para dentro e para fora do espaço entre cada par de bobinas, alterando assim a indutância e excitando as oscilações.