Alimentação elétrica trifásica: ativa, reativa, completa

Os valores da potência ativa total e potência reativa total do circuito trifásico são iguais às somas das potências ativa e reativa para cada uma das três fases A, B e C, respectivamente. Esta afirmação é ilustrada pelo seguinte fórmulas:

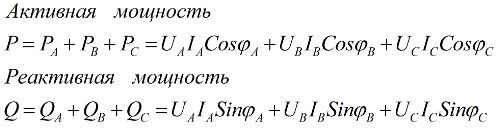
aqui Ua, Ub, Uc, Ia, Ib, Ic são os valores das tensões e correntes de fase e φ é o deslocamento de fase.

Quando a carga é simétrica, ou seja, em condições onde as potências ativa e reativa de cada uma das fases são iguais entre si, para encontrar a potência total do circuito multifásico, basta multiplicar o valor da potência da fase por o número de fases envolvidas. A potência total é determinada com base nos valores obtidos de seus componentes ativos e reativos:

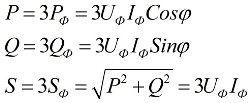
Nas fórmulas acima, os valores de fase das quantidades podem ser expressos em termos de seus valores lineares, que serão diferentes para esquemas de conexão em estrela ou triângulo para usuários, mas as fórmulas de potência serão as mesmas:

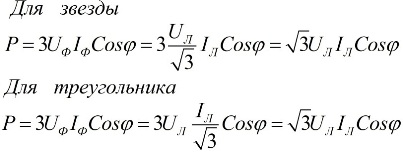
Resulta das expressões acima que independentemente do esquema de conexão dos receptores de energia elétrica, seja um triângulo ou uma estrela, se a carga for simétrica, então as fórmulas para encontrar a potência terão a mesma forma, tanto para um triângulo e para uma estrela:

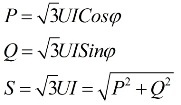
Essas fórmulas mostram valores lineares de tensão e corrente e são escritas sem subscritos. Normalmente, essa notação é encontrada, sem subscritos, ou seja, se não houver subscritos, significa valores lineares.

Um dispositivo de medição especial, chamado wattímetro… Suas leituras são determinadas pela fórmula:

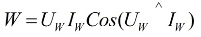
na fórmula acima, Uw e Iw são os vetores da tensão aplicada à carga e a corrente que flui através dela.

A natureza da carga ativa e o diagrama de conexão de fase podem ser diferentes, portanto, dependendo das circunstâncias específicas, os diagramas de conexão do wattímetro serão diferentes.

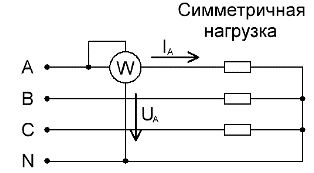
Para circuitos trifásicos carregados simetricamente, para uma medição aproximada da potência ativa total, se não for necessária alta precisão, um wattímetro conectado a apenas uma das fases é suficiente. Depois disso, para obter o valor da potência ativa de todo o circuito, resta multiplicar as leituras do wattímetro pelo número de fases:

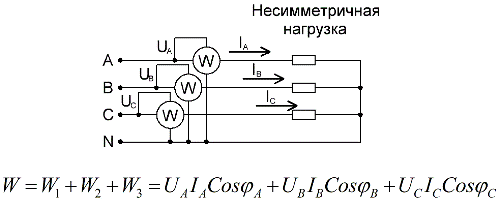
Para um circuito de quatro fios com um fio neutro, para medir com precisão a potência ativa, são necessários três wattímetros, cada um dos quais é lido e somado para obter um valor para a potência total do circuito:

Se não houver fio neutro em um circuito trifásico, dois wattímetros são suficientes para medir a potência total, mesmo que a carga esteja desequilibrada.

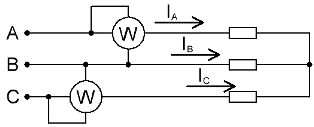
Na ausência de um condutor neutro, as correntes de fase são interligadas de acordo com a primeira lei de Kirchhoff:

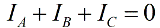
Então a soma das leituras de um par de wattímetros será igual a:

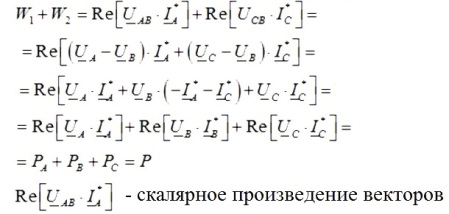
Portanto, se você adicionar as leituras de um par de wattímetros, obterá a potência ativa total no circuito trifásico em estudo, e as leituras dos wattímetros dependerão tanto do tamanho da carga quanto de sua natureza.

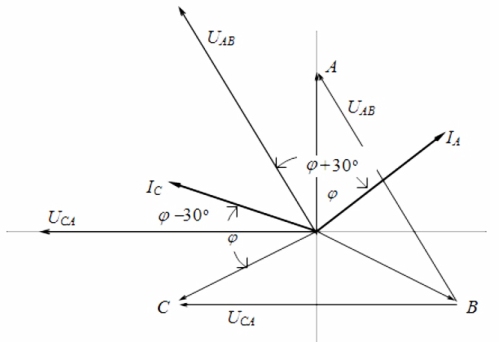
Olhando para o diagrama vetorial de correntes e tensões em conexão com uma carga simétrica, pode-se concluir que as leituras dos wattímetros são determinadas pelas seguintes fórmulas:

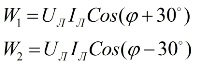
Após analisar essas expressões, pode-se entender que com uma carga puramente ativa, quando φ = 0, as leituras dos dois wattímetros serão iguais entre si, ou seja, W1 = W2.

Com indutância de carga ativa, quando 0 ≤ φ ≤ 90°, as leituras do wattímetro 1 serão menores que as do wattímetro 2, ou seja, W1 60°, as leituras do wattímetro 1 serão negativas, ou seja, W1 <0.

Com a natureza ativo-capacitiva da carga, quando 0 ≥ φ≥ -90 °, as leituras do wattímetro 2 serão menores que as do wattímetro 1, ou seja, W1> W2. Em φ <-60 °, as leituras do wattímetro 2 ficarão negativas.