Triângulos de tensões, resistências e potências

Qualquer pessoa que tenha uma ideia de diagramas vetoriais notará facilmente que um triângulo de tensão em ângulo reto pode ser claramente distinguido neles, cada lado do qual reflete: a tensão total do circuito, a tensão da resistência ativa e a tensão na reatância.

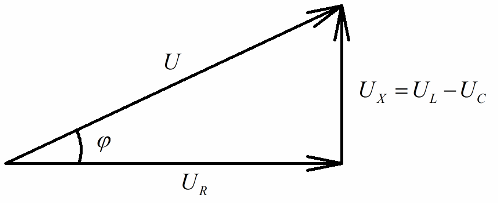
De acordo com o teorema de Pitágoras, a relação entre essas tensões (entre a tensão total do circuito e a tensão de suas seções) ficará assim:

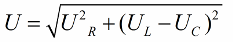
Se o próximo passo for dividir os valores dessas tensões pela corrente (a corrente flui igualmente por todas as seções do circuito em série), então por lei de ohm obtemos os valores de resistência, ou seja, agora podemos falar de um triângulo retângulo de resistências:

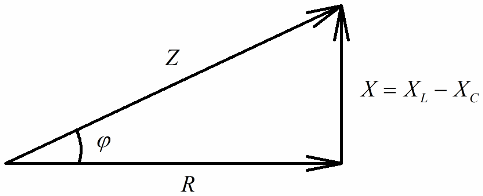
De forma semelhante (como no caso das tensões), usando o teorema de Pitágoras, é possível estabelecer uma relação entre a impedância do circuito e as reatâncias. A relação será expressa pela seguinte fórmula:

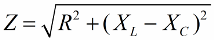
A seguir multiplicamos os valores da resistência pela corrente, na verdade vamos aumentar cada lado do triângulo retângulo um certo número de vezes. Como resultado, obtemos um triângulo retângulo com capacidades:

A potência activa libertada na resistência activa do circuito associada à conversão irreversível de energia eléctrica (em calor, na execução de trabalhos na instalação) estará claramente relacionada com a potência reactiva envolvida na conversão reversível de energia (a criação de campos magnéticos e elétricos em bobinas e capacitores) e com potência total fornecida à instalação elétrica.

A potência ativa é medida em watts (W), potência reativa — em varis (VAR — volt-ampère reativo), total — em VA (volt-ampère).

De acordo com o teorema de Pitágoras, temos o direito de escrever:

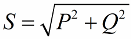
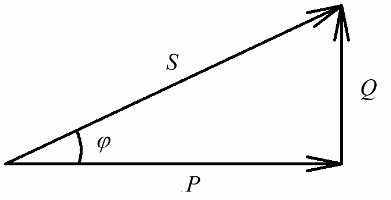
Vamos agora prestar atenção ao fato de que no triângulo das potências existe um ângulo phi, cujo cosseno é fácil de determinar principalmente pela potência ativa e pela potência aparente. O cosseno deste ângulo (cos phi) chamado fator de potência. Ele mostra quanto da energia total é contabilizada ao fazer um trabalho útil em uma instalação elétrica e não é devolvida à rede.

Obviamente, um fator de potência maior (máximo um) indica uma maior eficiência de conversão da energia entregue à usina para operação. Se o fator de potência for 1, toda a energia fornecida é usada para realizar trabalho.

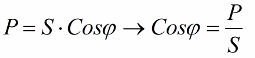
Os rácios obtidos permitem expressar o consumo de corrente da instalação em termos de fator de potência, potência ativa e tensão de rede:

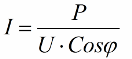
Assim, quanto menor o cosseno phi, mais corrente é necessária para a rede realizar um determinado trabalho. Na prática, esse fator (corrente máxima da rede) limita a capacidade de transmissão da linha de transmissão e, portanto, quanto menor o fator de potência, maior a carga da linha e menor a largura de banda útil (o cosseno phi baixo leva à restrição). As perdas Joule em linhas de energia com cosseno phi decrescente podem ser vistas a partir da seguinte fórmula:

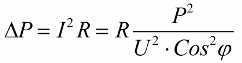
Na resistência ativa R da linha de transmissão, as perdas aumentam tanto mais quanto maior a corrente I, mesmo sendo reativa à carga. Portanto, podemos dizer que com um baixo fator de potência, o custo da transmissão de eletricidade simplesmente aumenta. Isso significa que aumentar o cosseno phi é uma importante tarefa econômica nacional.

É desejável que a componente reativa da potência total se aproxime de zero, para isso seria bom usar motores elétricos e transformadores sempre em plena carga e desligá-los ao final do uso para que não fiquem ociosos. Sem carga, motores e transformadores têm um fator de potência muito baixo. Uma maneira de aumentar o cosseno phi nos usuários é usar bancos de capacitores e compensadores síncronos.